DFS I

Depth First Search is a searching algorithm based on tree or graph. Essentially, it starts from a root node, traverse each child node. It is a root node for each child node. And find the result while traversing all possible branches/nodes.

Article Language: Chinese
Example Language: Java
Reading Time: 12min

Depth First Search 是一种基于树状(Tree) 或者图状(graph)的搜索算法, 本质是从一个节点(root)出发, 向每一个分支进行搜索, 而对于每一个分支来说, 它本身就是一个节点, 从这个节点继续向它可能产生的分支进行搜索, 最终在搜索所有的可能性的过程中找到结果. 也就是所谓的普遍撒网吧.

SubsetI
SubsetII
Partition an Array into K Equal sum subsets
Combination of K I
Combination of K II
Combination of Coins
Combination of Factors
PermutationI
PermutationII
Valid ParenthesesI
Valid ParenthesesII
N-QueenI
N-QueenII

Subset I

input: A linear data structure, such as an array or a string.
output: A list of lists of all unique subsets.

DFS 的核心就是回溯( backtracking), 也就是说, 这些分支从哪里来的, 最后清除了沿途附加的状态再回到哪里去.

dfs 可以使用 for 循环来控制 recursion 的层数.
在这里, for 循环的终止条件就是 dfs 的终止条件.
局部变量 i 作为参数 index 传入函数 dfs, 当 i 等于 input 的长度的时候, 函数返回.
其实和普通的 for loop 是一样的, 只要明白 index 和 i 分别表示的是什么. 这里在最外层的 for loop 执行了 n 次, n 是 input 的长度, 而每一次调用的时候 i 进行了一次 + 1 的操作, i 次调用的 dfs 中的 for loop 会执行 (n - i) - i 次, 同样的, 当 i 的长度等于 input 的长度的时候函数返回, 一次退回上一层调用它的那个循环中, 再继续.

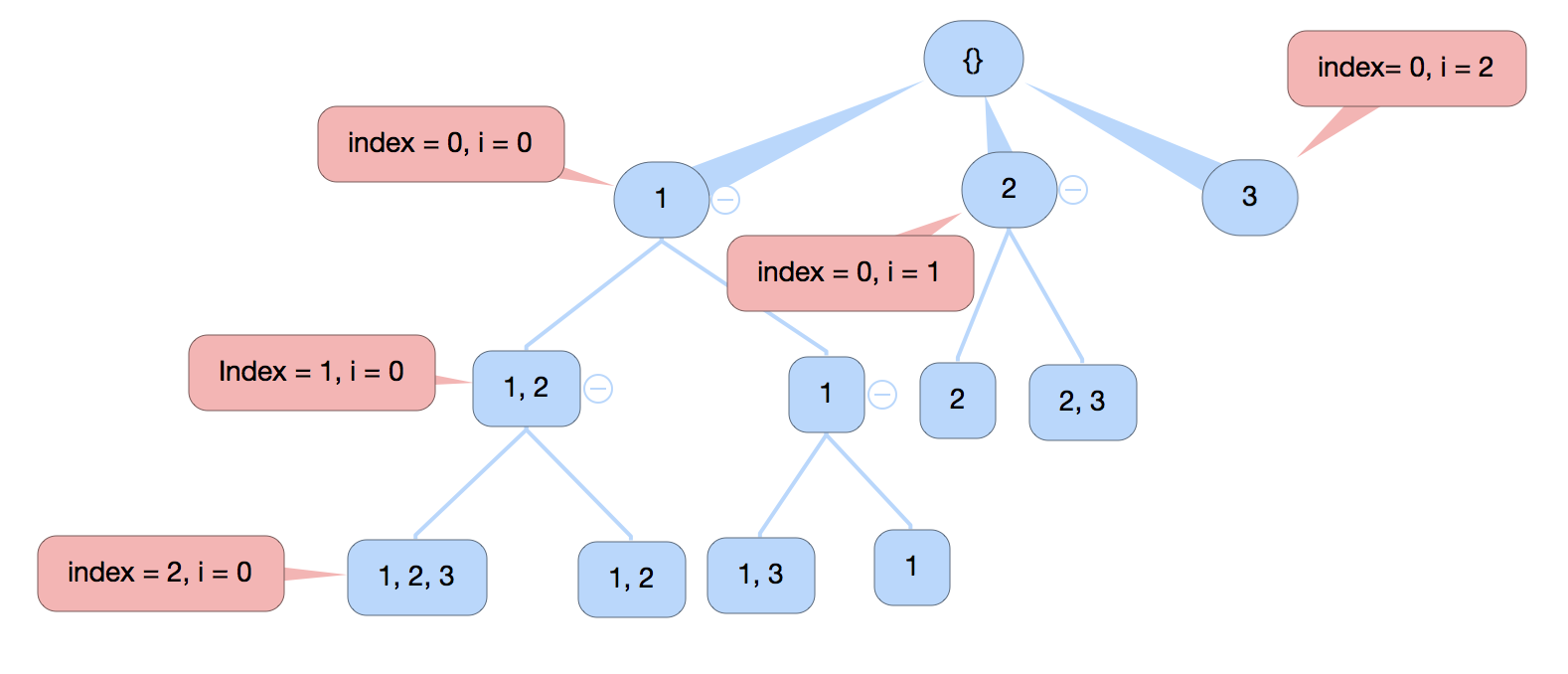
For a position i in the input, it has (n - i) - i (where n - i is the size of sub-problem, f(n - 1))choices to run, where n is the length of the input. Every time when the dfs is being called, the size of the problem reduces to n - i, therefore T(n) = 2T(n - 1), O(2^n).
Since it’s recursion, the call stack would be the length of the input, which is O(n).

代码如下:

class Subsets {
  public List<List<Integer>> findSubsets(int[] input) {
  	if (input == null) {
  		return new ArrayList<>();
	  }

	  if (nums.length == 0) {
	  	results.add(new ArrayList<Integer>());
	  	return results;
	  }

	  List<List<Integer>> res = new ArrayList<>();
	  dfs(input, 0, new ArrayList<>());
	  return res;
  }

  private void dfs(int[] input,
  		int index,
  		ist<Integer> subSolution,
  		List<List<Integer>> result){

  	result.add(new ArrayList<Integer>(subSolution));

	for (int i = index; i < input.length; i++) {
	  	subSolution.add(input[i]);
	  	dfs(input, i + 1, result);
	  	subSolution.remove(sobSolution.size() - 1);
	}
  }
}

首先如果不是用 for 循环来控制 recursion 的层数, 那么 recursion 就一定需要一个退出条件.
也可以使用 for loop 来每一层的状态, 或者说每一个位置上的可能性, 或者每一个元素可能产生的分支个数等等. 那么 dfs 的终止条件就不再是 for 循环的终止条件了, 而需要明确的写出来. 通常是当下标指向了 input 长度 + 1 的位置的时候.
那么局部变量 i 表示的就是对于当前下标来说, 它有几种选择, 只是 i 不再代表可选择元素的下标了. 所以参数需要使用 index.
for loop 的意义是在以当前 index 为节点调用 2 次 dfs, 如果 i 是 0 的话, 加上 index 对应的元素, i = 1 时返回上一层的状态, 并且进行下一次的递归调用 (也就是不加的情况).

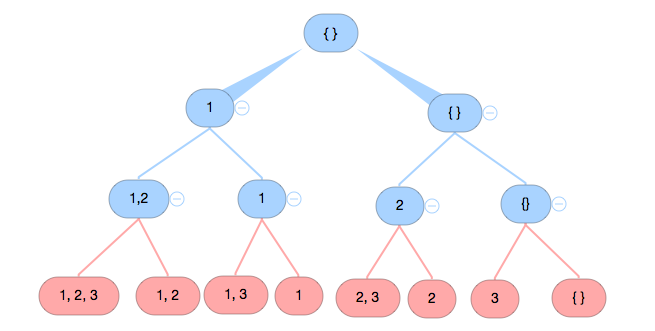
For element in a position i, it has two states, eighter added or removed. The it has n positions, where n is the length of the input. Thus, time complexity is 2^n.
Space complexity is the call stack layers, which is O(n).

代码如下,

private void dfs(int[] input,
	int index,
	List<Integer> subSolution,
	List<List<Integer>> result) {

  if (index == input.length) {
      result.add(new ArrayList<>(subSolution);
      return;
  }
  for (int i = 0; i <= 1; i++) {
	 if (i == 0) {
	   subSolution.add(input[index]);
	 } else {
	 	subSolution.remove(subSolution.size() - 1);
	 }
	 dfs(input, index + 1  , result);
  }
}

因为只有 2 种状态, 所以其实不需要一个 for 循环.

private void dfs(int[] input,
	int index,
	List<Integer> subSolution,
	List<List<Integer>> result) {

	if (index == input.length) {
		result.add(new ArrayList<>(sobSolution))
	}

	subSolution.add(input[index]);
	dfs(input, index + 1, subSolution, result);

	subSolution.remove(sobSolution.size() - 1);
	dfs(input, index + 1, subSolution, result);
}

Subset II

有重复元素怎么办?通常有两种解决方案,

排序
HashSet/HashMap(根据具体要求)

因为 dfs 的时间复杂度一定是高于排序的, 所以在时间复杂度上面没有区别. 空间复杂度来说, 如果是一个 array, 那么排序的空间复杂度就是 call stack 的层数, 如果是一个 String, 那么排序就一定要把 String 转换成 array 之后再排序. 所以就具体情况具体分析吧.

排序的方法

这里就用到了 Subset I 里面对于 index 和 i 的物理意义的分析, 当 i == index 的时候是在当前层第一次进入 for loop 的情况, 之后在调用 dfs 的时候, 把 i 所在元素的后一个元素当做 index 参数传给 dfs. 所以当函数返回之后, local 变量被 GC, i 依然是作为 for loop 的自增变量存在.
所以对于一个排序的数组来说, 只有在当前层 for loop 第一次循环的时候 i 和 index 指向的是同一个元素.
那么当 index 和 i 不是指向同一个元素的时候( i 自增循环), 如果 index 和 i 下标指向的元素依然相同, 就说明是重复元素, 那么久可以直接跳过(不选的情况).
简而言之, 只有满足某种条件才从当前节点出发, 调用 dfs.

代码如下:

public dfs(int[] input,
	int index,
	List<Integer> subSolution,
	List<List<Integer>> result) {

	result.add(new ArrayList<>(subSolution));

	for (int i = index; i < input.length; i++) {
		if (i != index && input[i] != input[i - 1]) {
		///i != index 保证了不会越界, 即使 index == 0 的情况.
			subSolution.add(input[i]);
			dfs(input, i + 1, subSolution, result);
			subSolution.remove(subSolution.size() - 1);
		}
	}
}

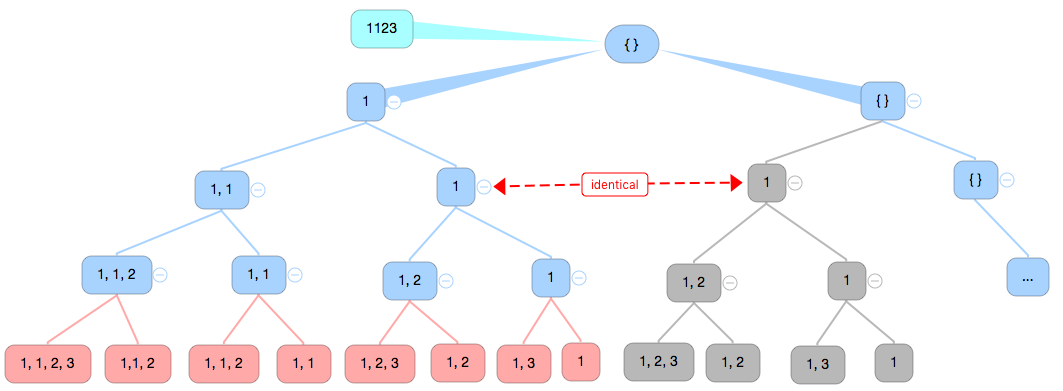
如果不使用 for 循环作为递归调用的终止条件判断, 基于对每一层传入参数 index 的选取, 它的树状结构应该是这样的.
可以看到, 以一个重复元素为节点展开的递归调用所产生的 subset 是和它第一次出现的节点的 subset 完全一致. 那么在当前层判断 index 是否第一次出现, 如果是, 那么就跳过.

代码如下:

public dfs(int[] input,
	int index,
	List<Integer> sub,
	List<List<Integer>> result) {

	if (index == input.length()) {
		result.add(new ArrayList<>(sub));
		return;
	}

	sub.add(input[index]);
	dfs(input, index + 1, sub, result);

	sub.remove(sub.size() - 1);
	while (index + 1 < input.length && input[index] == input[index + 1]) {
		index++;
	}
	dfs(input, index + 1, sub, result);
}

HashSet 的方法

假设重复元素只保留一个, 那么自然的想到可以把使用过的元素放到 HashSet 里面.
需要注意的是, 当我们返回上一层的时候, 有可能还会用到之前取过的元素, 那么这个 HashSet 就只能作用在当前层.
也就是说, 当 index 作为 node 传入的时候, 没进入一次 for loop 就会形成一个新的 HashSet, 当函数返回的时候, 所有当前层存在 set 里面的元素都不会被执行.

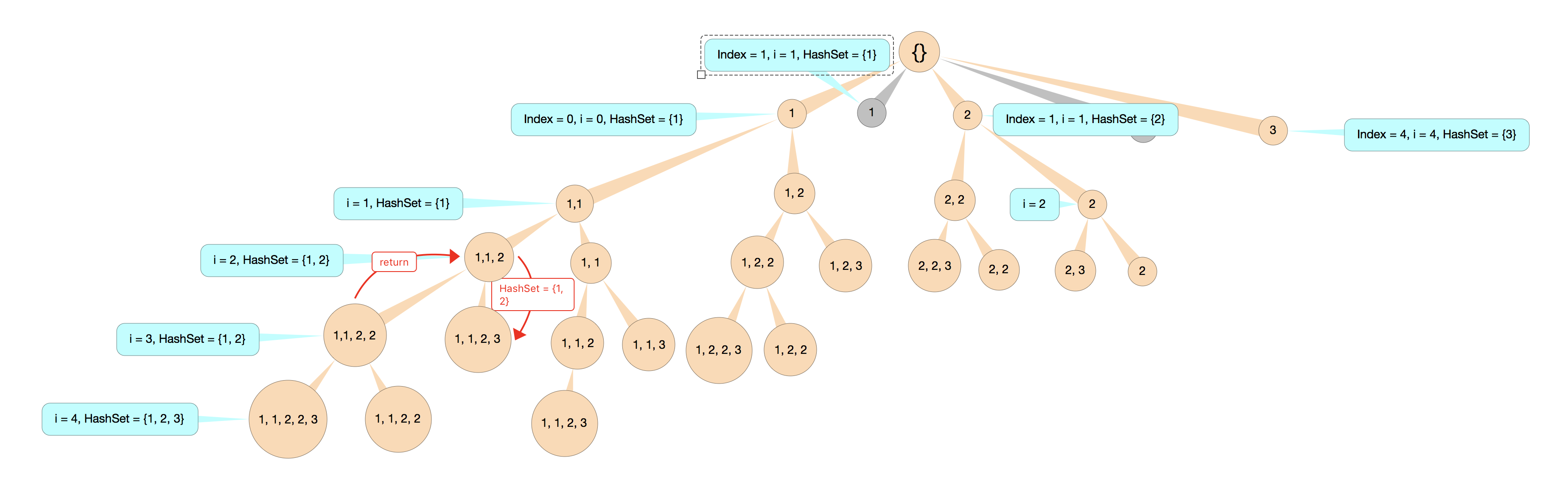
At each level, it runs n - i times looking for candidates, so the time comlexity would be as same as the regular subset.
However, if use a Hashset at each level to save visited elements, it would cost O(n^2) space.
代码如下:

public dfs(int[] input,
	int index,
	List<Integer> subSolution,
	List<List<Integer>> result) {

	result.add(new ArrayList<>(subSolution));

	HashSet<Integer> set = new HashSet<>();

	for (int i = index; i < input.length; i++) {
		if (set.add(input[i])) {
			subSolution.add(input[i]);
			dfs(input, i + 1, subSolution, result);
			subSolution.remove(subSolution.size() - 1);
		}
	}
}

Subsets 的解法有很多种, 最直观的是深度优先搜索(DFS), 另外也可以使用宽度优先搜索(BFS), 根据其特性,

对于每一个元素 e 来说都有 0 或者 1 两个状态
还可以使用 bit operation, 或者直接使用多层 for 循环, 每一层控制 2 个选择, 加元素与不加元素.
针对每一种 dfs 还可以有一些小小的 optimization. 暂且不表.

专注是优良品质, 这里就只写 dfs 了. 笔芯~❤